Rainbow tables

Intrigués par la rapidité avec laquelle une attaque par table arc-en-ciel (Rainbow table) permet de cracker l’empreinte (hash) d’un mot de passe, j’ai décidé de me plonger dans le sujet pour en savoir plus et comprendre « le truc ». Voici un petit résumé de mon voyage au pays des Rainbow tables.

Tout d’abord commençons par le commencement…

Méthode numéro 1 – La force brute

Toutes les fonctions de hachage communément utilisées sont telles qu’il n’existe pas de fonction inverse. Pour cracker une empreinte (hash), l’idée la plus simple est donc de prendre tous les mots de passes possibles, de calculer pour chacun son empreinte, et de la comparer à l’empreinte que l’on veut cracker. Si les deux empreintes sont identiques, on a trouvé le mot de passe, sinon on continue.

Empreinte recherchée : a7df33

aaaa => hachage => 6d8c33…Non, ce n’est pas celui que l’on recherche. Au suivant !
aaab => hachage => 54cd12…Au suivant !
aaac => hachage => af5a94…Au suivant !
aaad => hachage => a7df33…Gagné !! le mot de passe est « aaad »

Le problème avec cette méthode c’est que ca peut vite s’avérer assez long. Sur un PC moderne, il faut 8 à 10 jours de calcul en moyenne pour casser un mot de passe de 8 caractères alphanumérique (minuscules uniquement).

Méthode numéro 2 – Dictionnaire d’empreintes

Comme toujours en informatique, on peut aller plus vite, au prix d’une plus grande consommation mémoire. En effet, pourquoi ne pas calculer l’empreinte de tous les mots de passe possibles, puis stocker le tout dans un fichier ? Ensuite, pour cracker une empreinte, il suffit de chercher dans le fichier l’empreinte et de lire le mot de passe associé.

Empreinte recherchée: a7df33
Dictionnaire:

aaaa	6d8c33
aaab	54cd12
aaac	af5a94
aaad	a7df33
…
zzzz	8d6bc7

Le problème dans ce cas, c’est la taille du fichier. Une empreinte SHA-1 est composée de 20 octets, donc le fichier contenant les empreintes de tous les mots de passe de 8 caractères alphanumériques (minuscules uniquement) pèse déjà 50.000 Go, soit 100 disques durs de 500 Go !! Comptez 2000 disques de 500 Go pour stocker le dictionnaire des empreintes des mots de passe de 8 caractères alphanumériques (minuscules et majuscules).

Méthode numéro 3 – Rainbow tables

Les tables arc-en-ciel essayent de concilier taille de fichier et temps de calcul raisonnable.
Une attaque par Rainbow table (table arc-en ciel) se déroule en 2 étapes. Il faut tout d’abord générer une table, puis cracker une ou plusieurs empreintes à l’aide de cette table.

Génération de la table

Toute l’astuce des Rainbow tables consiste à calculer à partir d’une empreinte, un mot de passe. Attention, pas LE mot de passe qui correspond à l’empreinte (une telle fonction n’existe pas), mais UN mot de passe. On dit que l’on réduit l’empreinte. La seule chose que l’on demande à cette fonction de réduction c’est d’être cohérente, c’est-à-dire de toujours retourner le même mot de passe quand on lui donne la même empreinte en paramètre.

Le principe de génération d’une Rainbow table est donc le suivant: On part d’un mot de passe, on calcule son empreinte puis on calcule un nouveau mot de passe à partir de l’empreinte, on calcule l’empreinte de ce mot de passe, et on répète l’opération un certain nombre de fois. Ensuite on stocke dans la table le mot de passe initial et l’empreinte finale.

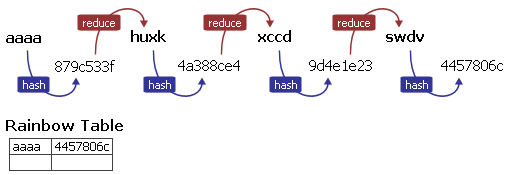
Puis on recommence le processus. On choisit un nouveau mot de passe, et on construit une nouvelle chaine.

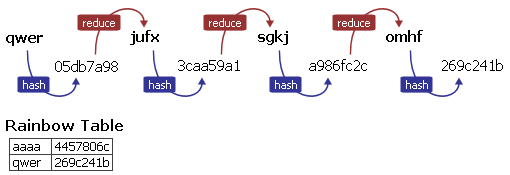
Voilà ! Nous venons de générer une Rainbow table contenant 2 lignes où chaque ligne représente une chaine de 4 mots de passe (chaine de longueur 4).

Utilisation de la table pour cracker des empreintes

Voyons maintenant comment utiliser cette Rainbow table pour cracker des empreintes.

Commençons par le plus facile : essayons de cracker l’empreinte « 269c241b ». Cette empreinte figure directement dans la table, à la seconde ligne, et est associée avec le mot de passe « qwer ». On sait donc que le mot de passe qui correspond à cette empreinte est le 4ème de la chaine. Malheureusement, on ne l’a pas stocké dans la table. Nous allons donc régénérer la chaine comme lors de la création de la Rainbow table. On prend donc le mot de passe initial, on le fait passer dans la fonction de hachage, ce qui donne 05db7a98. Ensuite on fait passer cette empreinte dans la même fonction de réduction que celle qui a servit à générer la table. Elle retourne donc le 2ème mot de passe de la chaine (jufx ) que l’on hache puis réduit pour trouver le 3ème mot de passe (sgkj), que l’on hache puis réduit pour donner le 4ème mot de passe: « omhf ». Bingo ! Pour être sur de nous, on hache « omhf », ce qui donne « 26c241b ». Re-bingo !! Nous avons cracké l’empreinte « 26c241b » : le mot de passe est « omhf ».

Essayons maintenant de cracker l’empreinte « 9d4e1e23 » : Pas de chance cette fois, cette empreinte ne figure pas dans la table. La partie n’est pas perdue pour autant ! Essayons de calculer une autre empreinte à partir de « 9d4e1e23 » : Un appel à la fonction de réduction nous donne « swdv », qui si on le passe à la fonction de hachage renvoie « 4457806c ». Oh surprise… cette empreinte figure dans la table à la 1ère ligne. Prenons donc le mot de passe initial « aaaa », et comme pour le premier cas, reconstituons la chaine : 2 coups de hachage/réduction nous donnent le mot de passe « xccd » qui une fois passé au hachoir donne « 9d4e1e23 ». Mission accomplie. Le mot de passe correspondant à notre empreinte est « xccd ».

Un dernier pour la route : « 05db7a98 » :

1. L’empreinte ne figure pas dans la table. Passons au plan B
2. reduce(hash(05db7a98)) => 3caa59a1. Qui ne figure pas non plus dans la table. Recommençons.
3. reduce(hash(3caa59a1)) => a986fc2c. Encore perdu. Recommençons.
4. reduce(hash(a986fc2c)) => 269c241b. Qui figure sur dans la table, à la 1ère ligne. De plus comme nous avons tourné 3 fois pour trouver, et que la table contient des chaines de longueur 4, le mot de passe recherché est le 1er de la chaine.
5. hash(qwer) => 05db7a98. C’est gagné !

Pour stocker 100 millions de mots de passe, il suffit donc par exemple de générer une Rainbow table contenant 100.000 lignes avec des chaines de longueur 1.000. On stocke donc dans un fichier de 2 Mo une table qui pèserait 2 Go dans le cas d’un simple dictionnaire… si on a de la chance et pas de collision!
Tout cela est trop un peu trop simple…
Car en pratique, les fonctions de réductions provoquent des collisions. Une collision survient quand la fonction de réduction retourne le même mot de passe pour deux empreintes différentes. Cela survient forcement car il y a toujours plus de mots de passes possibles que d’empreintes possibles.

Nombres de mots de passe de 8 caractères alphanumériques	(26+26+10)^8 = 52^8 = 5×10^13
Nombres d’empreintes SHA-1 (160 bits)	2^160 = 10^4

Reprenons l’exemple précédent et admettons que nous n’ayons pas eu de chance en ce début d’année 2008. Cela donnerait à peu près cela:

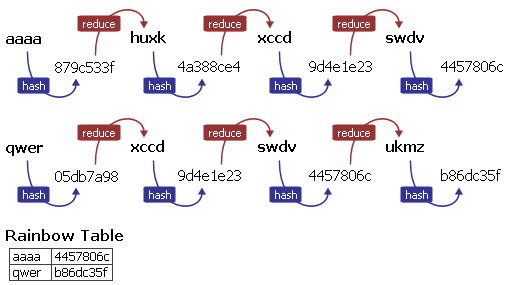
La collision se produit lors de la réduction de 05db7a98. La fonction retourne « xccd », comme pour l’empreinte 4a388ce4. Résultat : au lieu de contenir 8 mots de passe distincts, notre table n’en contient que 6. Nous avons des chaines qui sont dupliquées à partir de la collision (xccd => swdv).

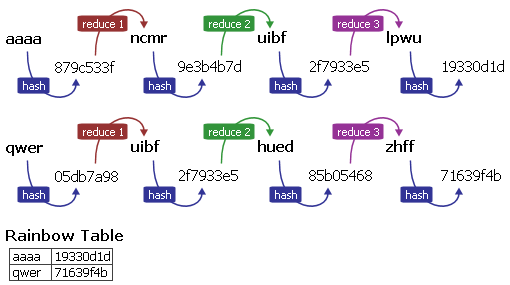
Pour diminuer cet effet indésirable, les Rainbow Tables utilisent non pas une mais plusieurs fonctions de réduction. En fait, il y a une fonction de réduction différente par « colonne ». Voici donc le schéma de génération d’une Rainbow table :

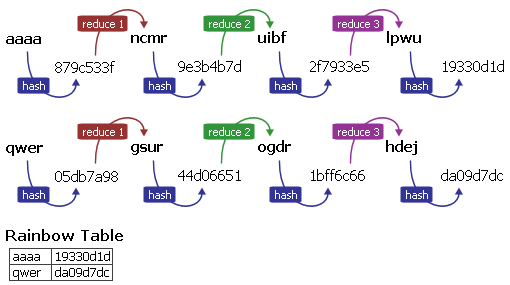
Cette fois, si une collision se produit, on ne se retrouve pas avec des chaines dupliquées car même si la fonction de réduction 1 retourne « uibf » pour l’empreinte 05db7a98, en haut on passe ensuite à la fonction de réduction 3, et en bas à la fonction de réduction 2, et donc au lieu d’avoir la chaine dupliquée jusqu’à la fin, on a juste un mot de passe dupliqué.

Voilà donc d’où ces tables tirent leur nom de tables en arc-en-ciel

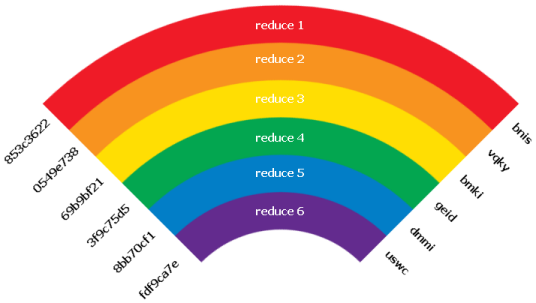
Evidemment dans le cas où on n’a vraiment pas de chance, on peut tomber sur une collision dans la même colonne. En pratique, ce cas n’arrive que peu fréquemment avec de longues chaines.

Si vous voulez aller encore un peu plus loin, vous pouvez regarder le code source d’un petit programme Java que j’ai écrit pour l’occasion qui génère des Rainbow tables pour casser les empreintes SHA-1 de mots de passe de 4 caractères alphanumériques (minuscules uniquement).

Télécharger la démo et les sources Java.